Gradient descent is a mathematical optimization method that serves as the backbone of most machine learning techniques. It allows us to find the minimum possible values of functions–known as minimizing a function.

This is particularly useful because many machine learning methods, especially neural networks, use something called the loss function to calculate how inaccurate their predictions are. It is essential to stress the underlying implication here: minimizing the loss function–therefore minimizing how wrong we are, is learning. Gradient descent is one of the simplest and most elegant ways learning is achieved.

Let’s delve deeper into what gradient descent is and how it works. After that, we’ll discuss possible modifications to gradient descent, as well as a basic implementation in Python. If you’re unsure about what machine learning is, check our previous article.

What is Gradient Descent?

First, let’s conceptualize the idea. Imagine that you are on a hill, blindfolded. You cannot remove the blindfold, but you want to go to the bottom of the hill. One simple way to achieve this is by feeling the ground beneath your feet and taking small steps downhill. Before each step, you assess the ground again and adjust your direction accordingly. This straightforward strategy will get you to the lower ground. Eventually, you will come to a point where, no matter which direction you attempt to go, it will be always uphill. You have reached a minimum.

In this example, the hill represents the function you are trying to minimize, the height represents the value of a function at a given point, and you are the gradient descent algorithm. The act of finding the steepest downhill direction corresponds to calculating gradients–a vector of a function that gives the direction and rate of the fastest increase (or decrease, in our case).

Now you know why it is called gradient descent; it is an algorithm that takes a small, descending step in the direction of the gradient.

The Part with Scary Symbols

Now that we have an intuitive understanding of gradient descent, let’s formally write the equation for it. We will introduce a new element called the learning rate, symbolized by γ, which you can think of as the size of the steps you take on the hill. We’ll denote our input parameters at step n as a_n, the function we want to descend as f(x), and the gradient of the function as ∇f(x).

We are subtracting the gradient because we want to move in the opposite direction of the greatest increase. You’ll notice that, because the next step f(a_n+1) depends on f(a_n), this is an iterative process. We start with a random point x₀, and we stop iterating once we observe no meaningful change in value.

Implementation in Python

Let’s dissect what we want gradient descent to achieve so we can instruct our computer to calculate it. It’s an iterative process, so we will use some sort of loop. We want our loop to stop once we stop observing a meaningful difference–or if it hits a depth limit, just to be on the safe side.

Within the function, we will apply the formula we mentioned earlier and then calculate the difference caused by our step. We can then advance our depth and a_n parameters. The full gradient descent function will look like this:

def gradient_descent(x0, learning_rate, convergence_criteria, depth_limit):
  
  # Initialize the parameters
  depth = 0
  difference = 2 * convergence_criteria
  x = x0  # x0 is our initial guess
  
  # As long as we are making progress and haven't exceeded the depth limit,
  # iterate through the function
  while difference > convergence_criteria and depth < depth_limit:
    x_next = x - learning_rate * derivative_of_f(x)
    
    # Calculate how much the value of the function has changed
    difference = abs(f(x_next) - f(x))
    
    # Advance the parameters for the next iteration
    x = x_next
    depth += 1

Note that code works for single-variable functions, but it can be trivially generalized to higher dimensions by using partial differentials.

Examples

Basic Parabola

We can start with a basic parabolic function and its first derivative, which gives us its gradient:

You can see how it looks in our code:

# Necessary imports for this code block
import numpy as np

# Simple Parabolic Function
def f(x):
  return x ** 2

def derivative_of_f(x):
  return 2*x

# Domain of the function
x_domain = np.arange(-5, 5, 0.01)

# Perform Gradient Descent
learning_rate = 0.02
convergence_criteria = 1 * 10 **6
depth_limit = 1000

# Choose a random starting point
rng = np.random.default_rng()
x0 = rng.choice(x_domain)

gradient_descent(x0, learning_rate, convergence_criteria, depth_limit)

Plotting the function, as well as the path our gradient descent took using Matplotlib, we can visualize how our descent function works:

Multivariate Functions

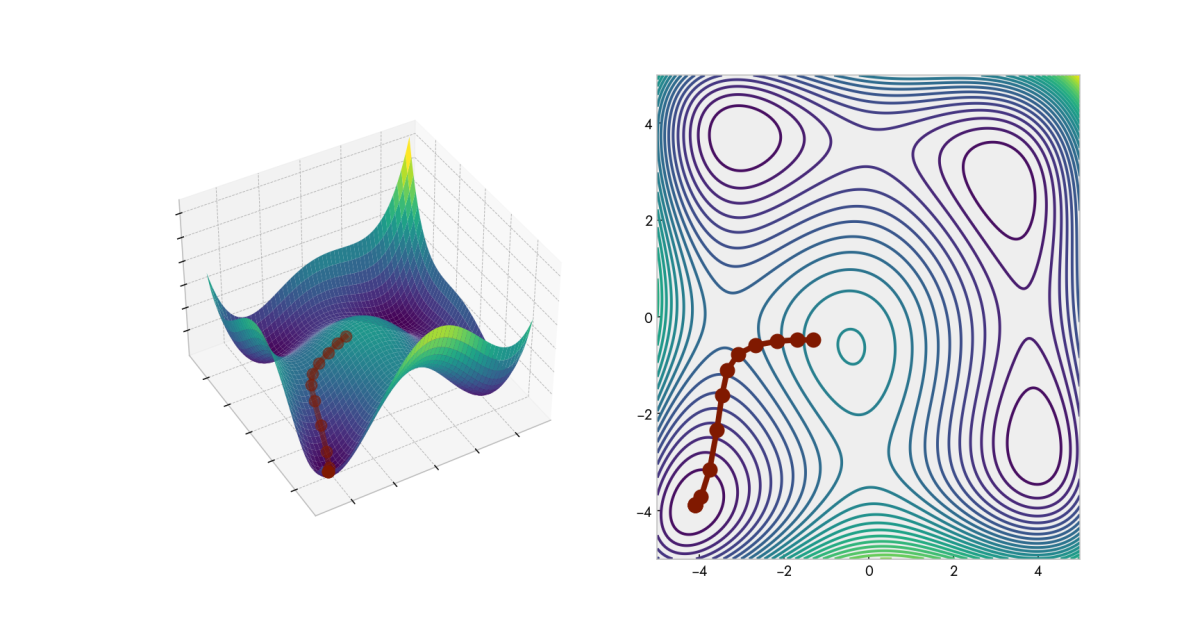
Parabolas are very simple functions with a single global minimum or a maximum. Many problems we encounter in real life are more complex than that. So let’s go a dimension higher and try a slightly modified Himmelblau’s function–a function that contains multiple minima:

The gradient of a multivariate function is composed of the partial derivatives for each variable:

We can adapt this function to our previous code with little modification. It should look as such:

Problems with Gradient Descent

Deciding Learning Rate

Learning rate is one of the most important hyper-parameters–that is, variables that externally tune the models and functions. Choosing too low of a learning rate will mean that gradient descent will need hundreds or thousands of steps to converge, if it converges at all. Conversely, if the learning rate is too high, you may start oscillating instead of converging.

That is why various approaches were developed to alter the learning rate dynamically. Momentum is one of the most common techniques; instead of letting the latest gradient decide the direction on its own, previous gradients are also taken into account, providing a form of inertia.

Decaying learning rates is another popular option, where the learning rate is dynamically reduced with more iterations. This allows the descent to start fast at first, covering large distances in the search space, but slow down and hone in on a minimum afterward.

Learning rate optimization is not a trivial problem. In machine learning, training large models can days and even weeks on state-of-the-art hardware that is expensive to operate. Choosing the right learning rate, or using one of the other approaches we discussed earlier, can save you time, energy and money.

Local vs Global Minimum

While our parabola had a single minimum, many functions contain multiple minima. In some cases, only one out of these minima is truly the lowest point–the global minimum. In such cases, every other minimum is a local one–a point that is lower than all its immediate neighbors.

For many real-life applications, determining whether we are on a local or a global minimum is not straightforward. In some cases, it is worth spending the extra resources to find the global minimum, while in others, settling on a local minimum may be sufficient.

Initialization

For many functions, our initial guess significantly impacts the path the gradient descent takes and the final destination it reaches. Depending on the application, finding the global minimum could be crucial. In such cases, conventional hyper-parameter tuning methods such as grid-search can be employed.

Gradient Descent in Machine Learning

In machine learning, we work with datasets instead of pre-defined functions. This means we must present our data in such a way that we can apply gradient descent. We will provide only a brief overview of this topic, as the details of this process will be discussed in other articles since it is outside the scope of this one.

In many cases, this linear relationship is achieved by establishing a linear equation between the output data and the input data in the form of:

Where X and Y are the input and output data of length N, while w and ß are (N, 1) vectors known as weights and biases, respectively.

We initialize the weights and biases and predict the output data using the equation. We can then look at the difference between our predicted output and the real output using the loss function mentioned at the beginning of the article. It is this loss function that we aim to minimize.

Modifications to Gradient Descent

One thing you may notice about this method is the fact that we used the entire input data during our optimization step. This is often impractical; we can easily have terabytes of training data, while our computers may have only gigabytes of RAM. Additionally, calculating the gradient for the entire dataset is computationally expensive. This standard version of gradient descent is called batch gradient descent in machine learning.

To address these issues, various optimizations to gradient descent were developed. Stochastic gradient descent replaces the actual gradient by approximating it from a single data sample instead. This greatly reduces both computation and memory requirements of the optimization but introduces instability, as descent no longer occurs in the steepest decrease direction of the entire dataset.

Another version of gradient descent, called mini-batch gradient descent, aims to achieve the best of both worlds. Instead of using the entire dataset or just one sample, it instead picks a small subset of samples each time, such as 32. This approach mitigates the instability introduced in stochastic form, while remaining much faster than the batch form. For these reasons, mini-batch gradient descent is the most commonly used form of gradient descent.

Closing Thoughts

Gradient descent and its derivatives are among the most critical algorithms in machine learning. Understanding the intricacies of this method, such as the behavior of the learning rate, can have a substantial impact on model training and can save you time and money. For this reason, a solid understanding of the subject is essential for every machine learning engineer or data scientist. I aimed to provide a comprehensive overview of gradient descent, and I hope it deepens your appreciation for this method.

In the future, we will delve deeper into other forms of gradient descent introduced here, as well as their immediate applications in machine learning pipelines. Until then, stay curious!